小孩总是无脑地设未知数和机械无脑地使用方程的毒已很深，需要禁止孩子不许他设未来知数和列方程来纠正吗？

举个例子，让你证明一道简单的初中数学题：任何一个圆的直径所对应的圆周角都是直角。

如下图， 为圆心， 为直径，也就是让你证明 为直角。

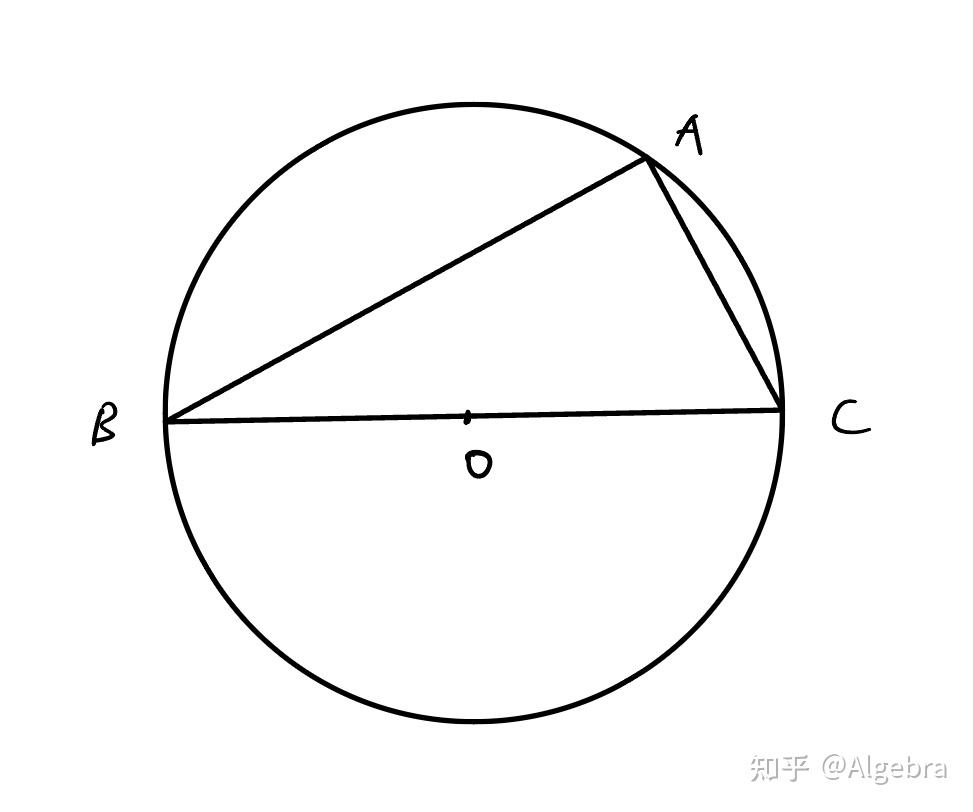
证明思路也很简单，我也不卖什么关子，就是连接 作一条辅助线。

注意到 ， ， 都是半径，所以 与 都是等腰三角形，也就是说明

，我们不妨记为 ；同理，我们有 。

如图所示：

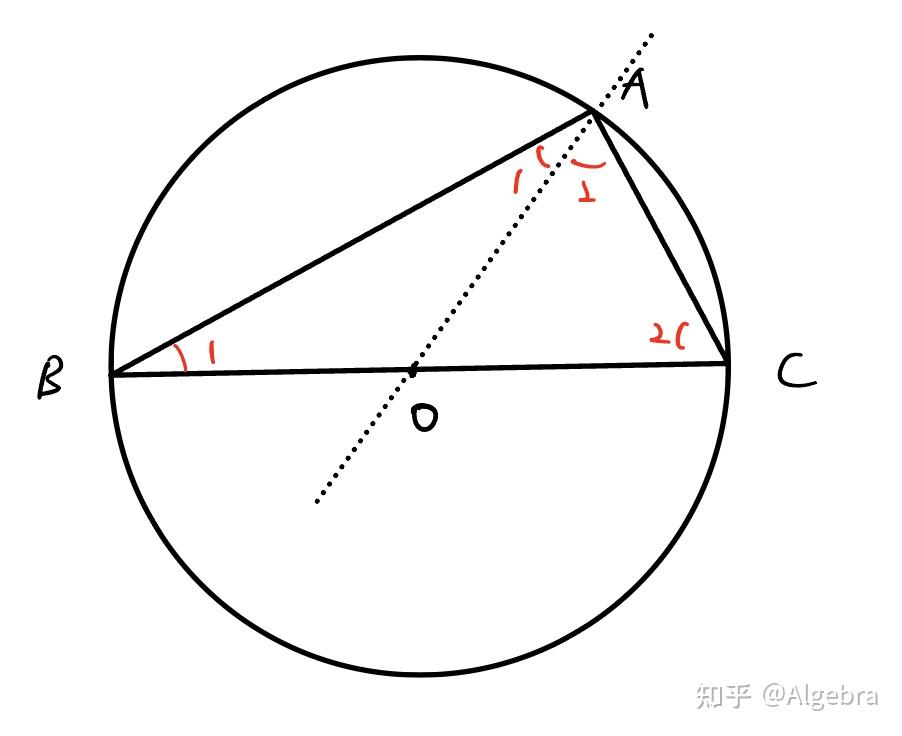
又因为三角形的内角和为 ，故 。

故

所以 ，得证。

证明过程并不难，但相信你应该观察到了，整个证明最核心的一步就是构建一条辅助线 ，倘若没有那么一丝的灵感，这道题并不是特别好做。

也就这道题的辅助线不是特别难构造，所以这道题并不复杂，回忆一下，从小学到初中，是不是有很多的几何题就是因为辅助线构造起来比较困难而导致没做出来呢？

那我们应该怎么办？去不停地做题使得我们去熟悉一切辅助线的构造方法？把我们短暂的一生投入到无限的辅助线练习中？

欧几里得写过一本书叫《几何原本》，里面有超级多的几何证明难题，很多都是靠着一个又一个精妙绝伦的灵感做出来的。

估计在题主看来，拼命的去练习这些所谓的“灵感”才是学数学的正道。

17世纪有一位数学家叫笛卡尔，他就对这种奇妙的灵感深感不安，他认为我们应该研究的是几何图形的本质，而不是一些可能谁也想不到的奇思妙想。

倘若一道题需要构造一条我们谁也想不到的辅助线该怎么办，是不是就永远做不出来了？

笛卡尔说：

“我决心放弃那个仅仅是抽象的几何，这就是说，不再去考虑那些仅仅是用来练习思想的问题。我这样做，是为了研究另一种几何，即目的在于解释自然现象（本质）的几何。”

“没有任何东西比几何图形更容易印入人脑，用图形表达事物非常有益；而代数中的公式可以使解题过程机械化，代数具有作为一门普遍的科学方法的潜力。”

于是，他将几何与代数结合了起来，建立了解析几何。

在笛卡尔之前，人们认为几何就是几何，代数就是代数，它们之间没有半毛钱联系。我们可以将几何与代数比作两座大海中的孤岛，而这两座孤岛上的人们说着不一样的语言，穿着不一样的衣服，有着不一样的风俗习惯。

笛卡尔想的是，我要在这两座孤岛间架起一座桥梁，顺便在桥上帮助两座岛上的人翻译对岸的语言文字。

一道几何难题，靠着几何岛上的工具非常难以解决，那我们可以将其翻译成代数岛上的人听得懂的语言，让他们去研究。

而在代数岛上，有着一整套几何岛上的人闻所未闻的新工具，在这些新工具的帮助下，或许原本几何岛所的难题在代数岛上就变得非常简单，最后我们再将代数岛上解决后的结论翻译回几何岛的语言，原本的难题就被解决了。

顺便说一下，数学家最喜欢的一件事就是架桥，比方说著名的费马大定理就是依靠谷山志村猜想解决的，谷山志村猜想本质就是在椭圆曲线（代数几何的对象）和模形式（某种数论中用到的周期性全纯函数）之间架起了一座桥。

我们再回过头看刚刚那道题，也就是证明 为直角。

我们要将这个几何问题转换为代数问题，毕竟直角什么的是几何学里的的东西，代数里没有。

于是我们引入斜率的概念，要证明 为直角本质上就是证明直线 的斜率乘以 的斜率是 。

那如何定义斜率呢？

于是笛卡尔就建立了平面直角坐标系，尝试用代数的语言来描述直线的倾斜角的大小。

我们再不妨设这个圆的半径为 ，那么在此坐标系下 点的坐标就为 ， 点的坐标为 ，又因为 点是圆上一点，我们可以设其坐标为 。

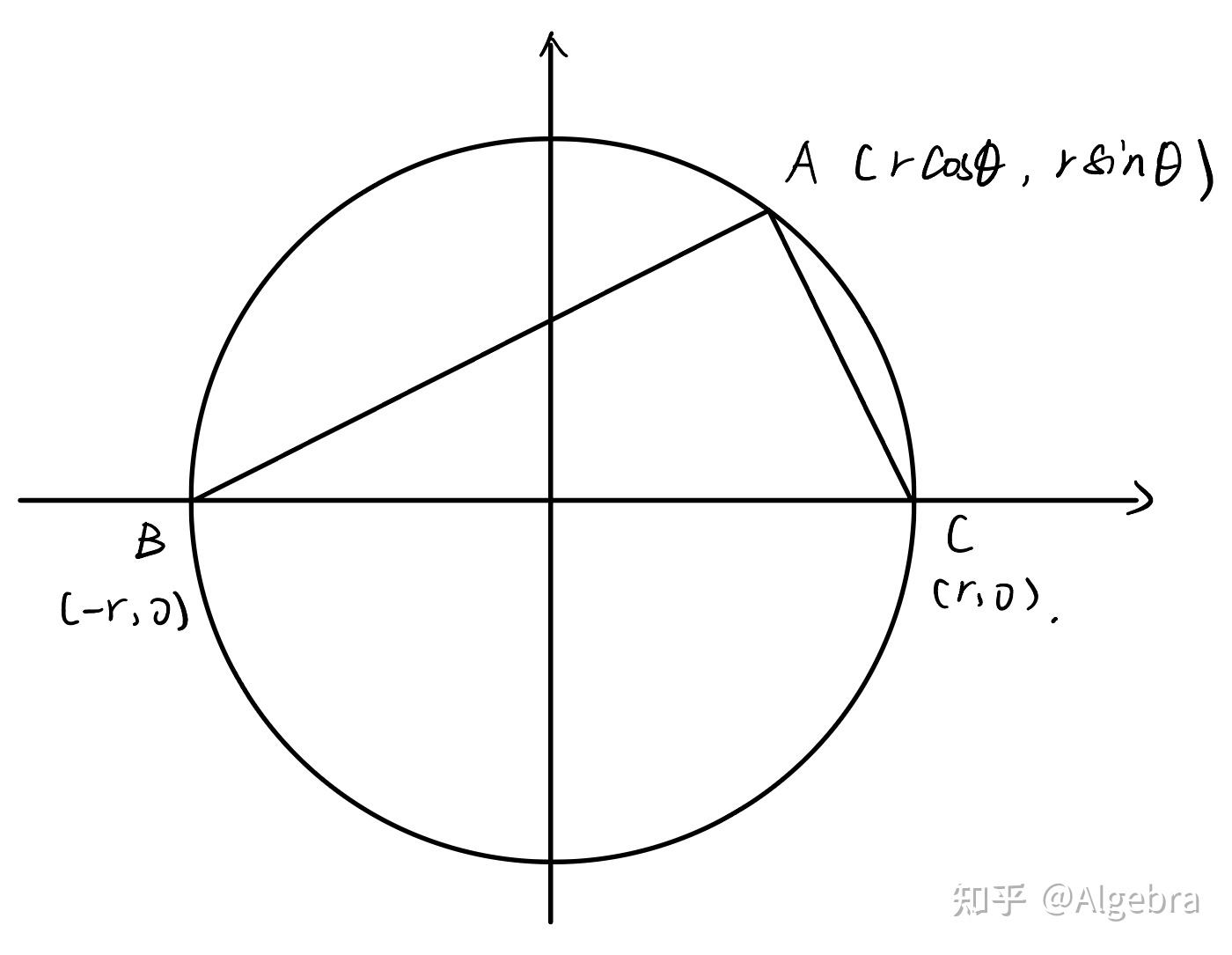
那么直线 的斜率 ，直线 的斜率为 。

则

这样我们就证明了 与 垂直，也就证明了 为直角。

或许有人会说，这样做相比于最初的证明好像更麻烦了，但不知道你有没有发现，这次我们压根没有画任何辅助线！

对的，解析几何就是将一个几何问题转化为一个代数方程，而解一个代数方程完全是机械性的，解完方程后，再将代数的解转化为几何的实际意义，这样就避免了靠奇思妙想构造辅助线的步骤。

笛卡尔在建立解析几何后，立马将其运用到《几何原本》中，发现此方法开始大杀四方，原本许多证明思路极其困难，或是构造非常巧妙的题目变得异常机械与显然。这一结果是颠覆性的，从此代数与几何的研究开始腾飞，也顺便促进了微积分的出现，数学开始走向近代。

高赞回答里有两句话我深表认同：

整个数学史，就是一个无数优秀的大脑不断地把各种问题变成一种可以无脑使用的形式系统的历史。
把一个看似复杂的问题，变成一种可以无脑运算的形式语言（也就是你所说的设未知数和列方程），是数学中相当高级的能力 —— 如果不是最高级的能力的话。