高中阶段自己独立思考硬刚写出来的题和直接看答案，二者效果上有什么区别?

数学有个特别有意思的地方，碰到一个难题你硬刚下去，可能会在许多莫名其妙的地方获得收货。

记得大一的时候有次算某道题的极限，泰勒展开三次方项算不出来，非得展开到四次方，当时我记很好奇，为什么？

它的本质是什么？

花了一个晚上，不停地构造一个又一个的极限，不停地尝试展开，揣摩它们的细微差别，后面发现了极限本质上是求其对应的幂级数最低次项前系数的比值。

如果没有这份好奇心，估计那道极限题过去了就过去了。

还有比如求某个函数在某一点的取值，方法很简单，就是泰勒公式，然后代值，但我当时就好奇，比方说这道题要求精确到小数点后两位，我究竟需要泰勒展开到多少项？

又是花了一个多小时，自己独立发现了收敛速度这一概念。

这是两个印象最深刻的硬刚了，还有很多次硬刚的过程虽然忘记了，但我知道每次硬刚后我的思维方式都不一样了，记得大一结束后的我就已经孤独求败了。

总结下来就是：你的那些思考看上去没什么用，但你的留下了数学思维，以及发现隐藏规律的能力。

你的所看所学都进了你的肚子里，消化后完全成为你身体的一部分，哪怕这道题你忘记了，但你的思维永远不会忘。

再举个这两天学抽代的一些经历吧，学完同构这一章后，后面的习题要我算出 的自同构群 。

说实话，这道题很简单，没什么大不了的。

但我在做完这道题后，就心血来潮想试一试 的自同构群 和内自同构群 。

当然，这也不是多难的问题：

到目前为止，都很正常。

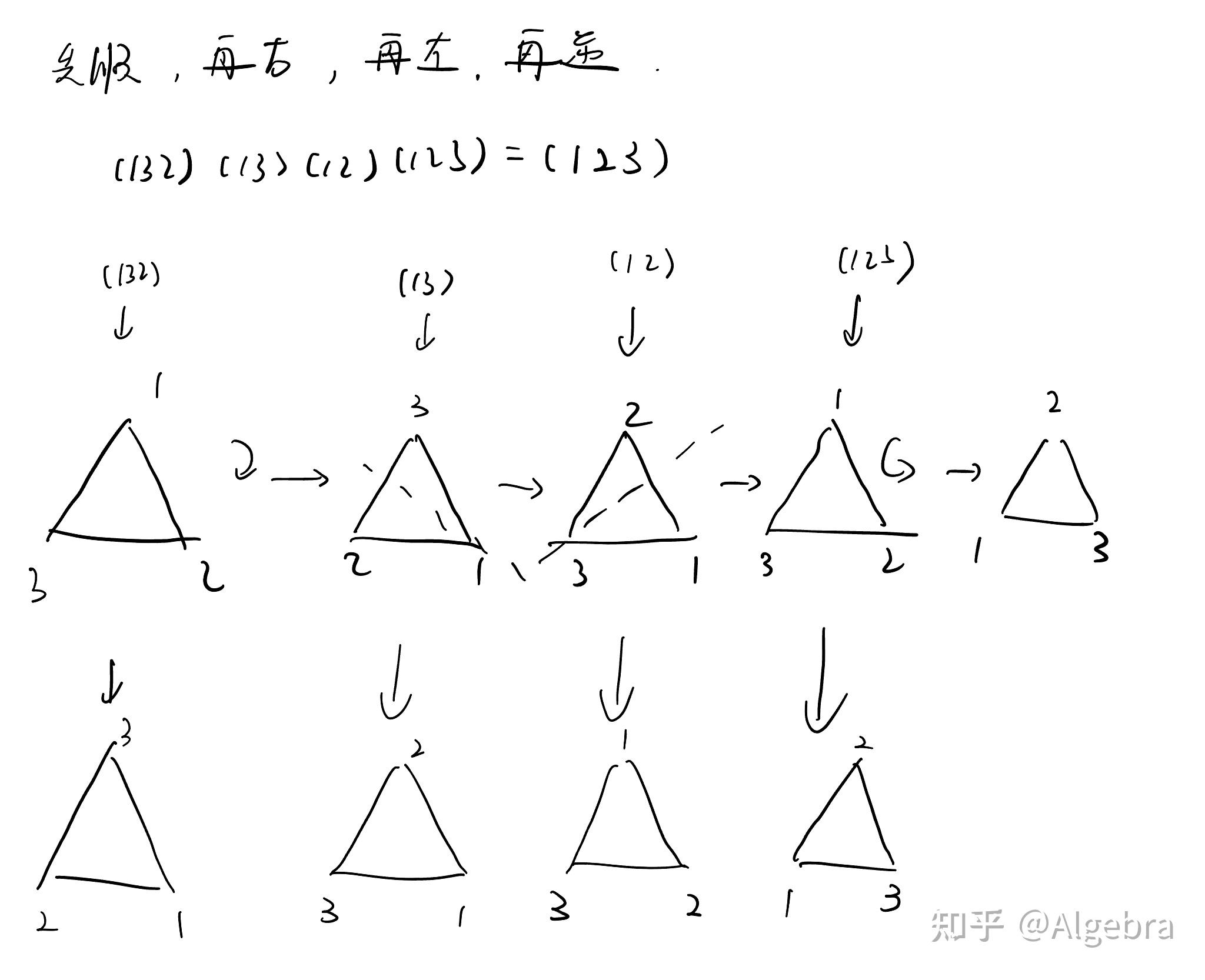
但我接下来冒出来一个念头，就是这个 我知道，可以看成一个等边三角形的六种变换：

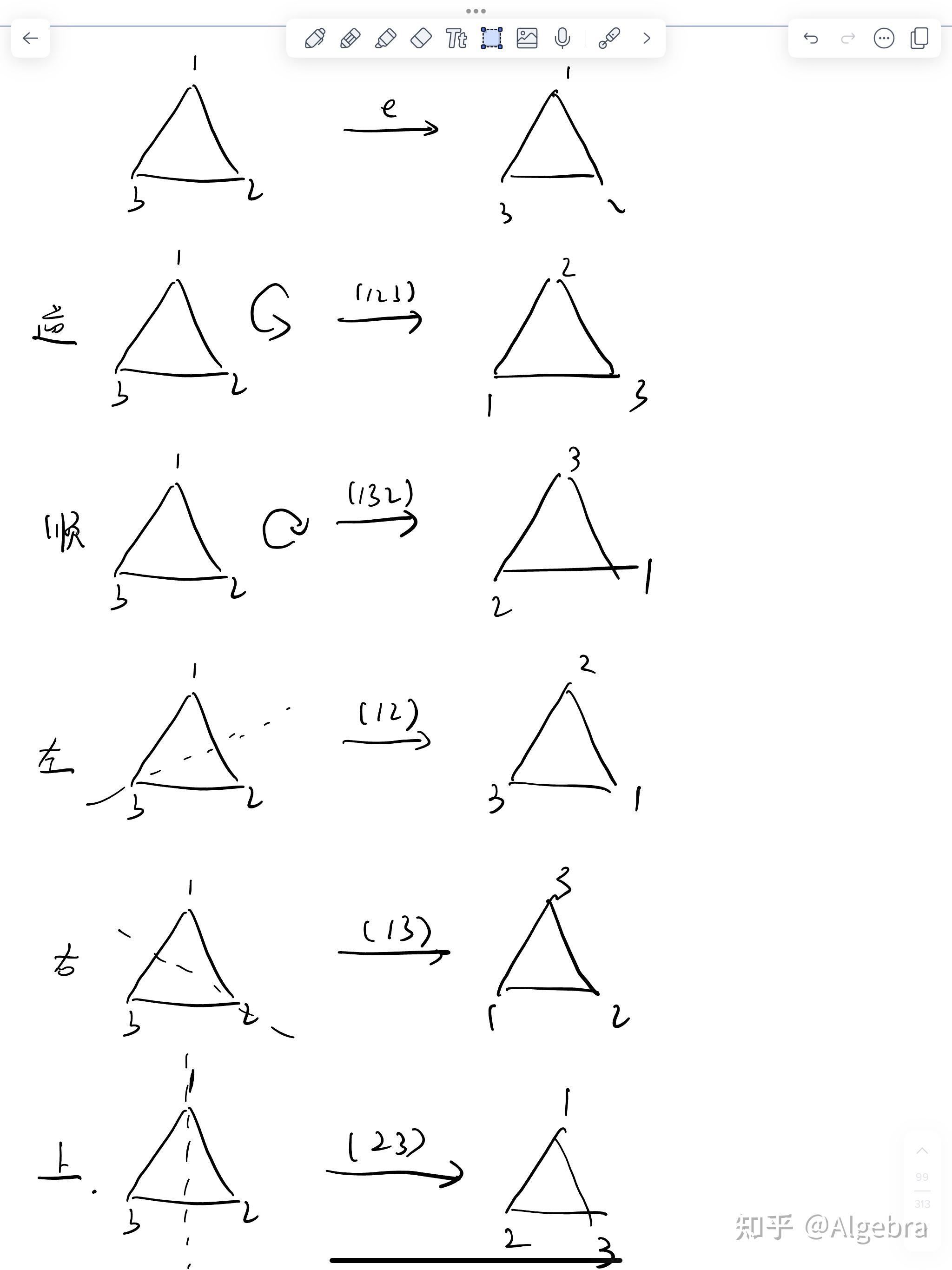
我给它们分别取了名字：不变，逆时针，顺时针，左翻转，右翻转，上翻转。

接下来我就在想，我把一个等边三角形先左翻转，再逆时针，结果是什么？

本来这似乎也不是个问题，左翻转是 ，逆时针是 ，所以无非就是算一下 ，按照习惯，我从右往左算，结果是 。

验证了一下，没错。

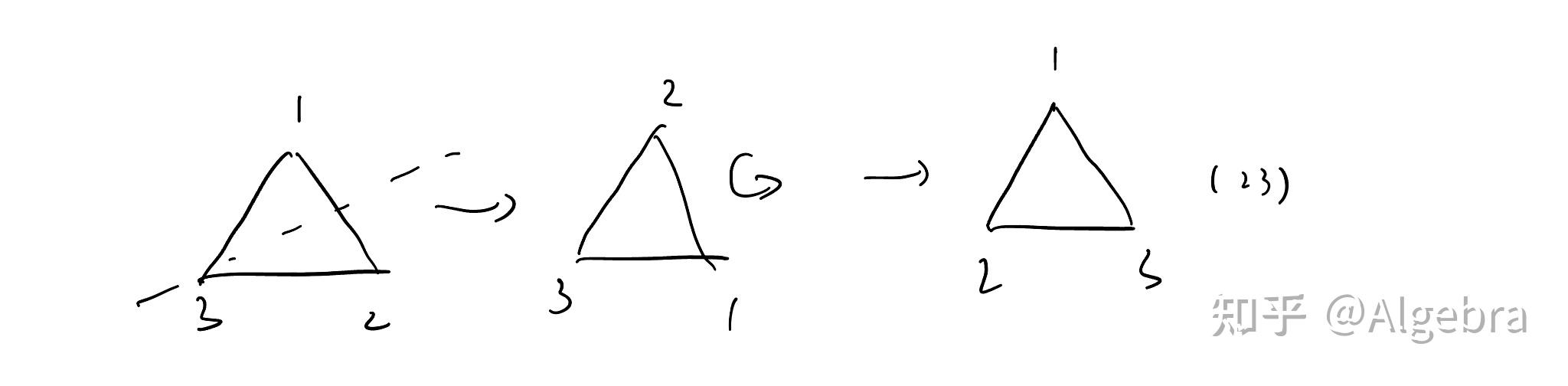
但在这一瞬间，我突然感觉到了一丝寒意，不是，为啥？

我为啥要从右往左算？

虽然结果是对的，但如果是从右往左算，岂不是我是先对等边三角形作用了逆时针 ，然后再作用左翻转 ？

可是我明明是先左翻转 ，再逆时针 啊！

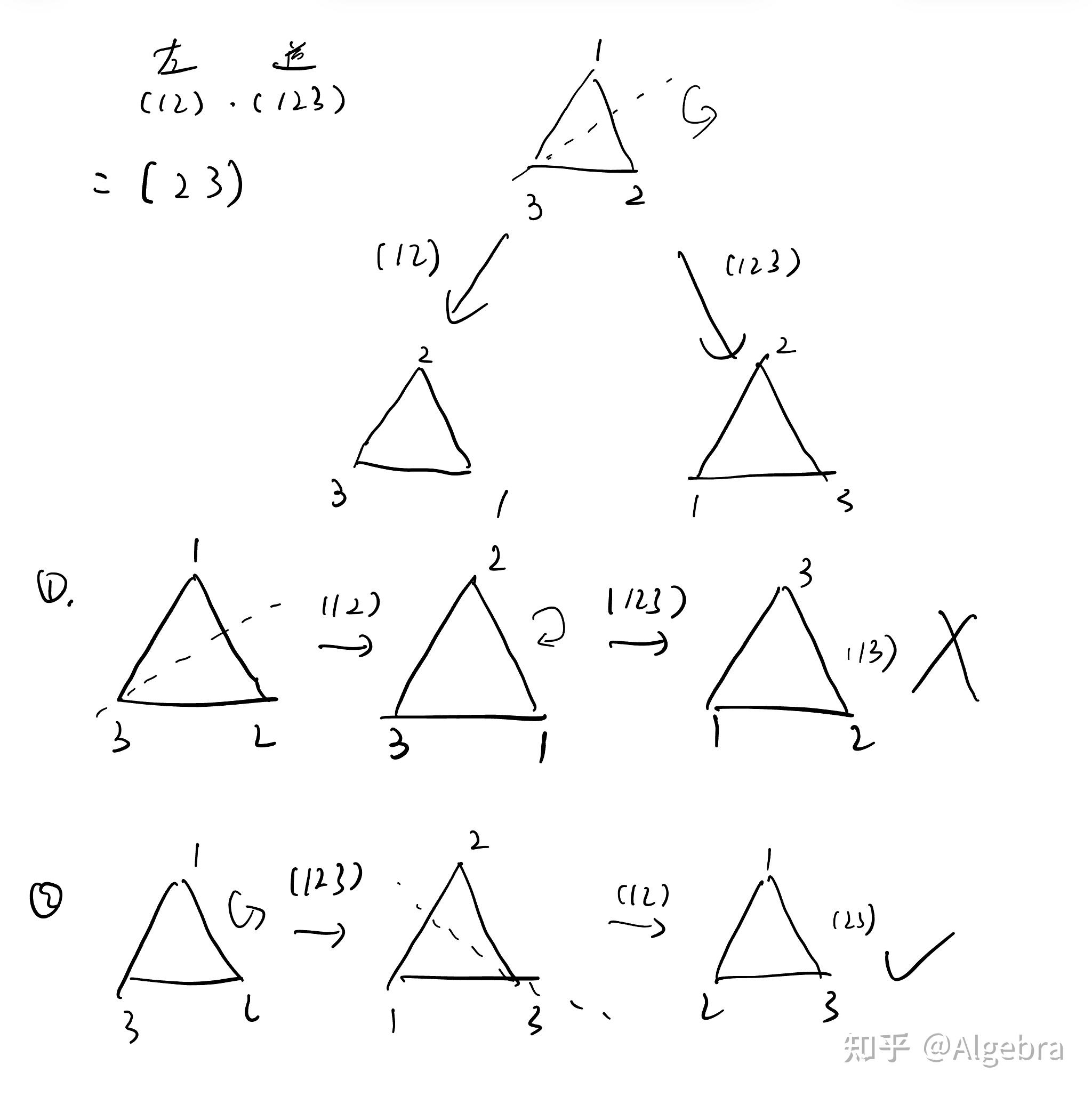
上面这幅图就是我分别尝试了先作用左翻转 ，和先作用逆时针 的情况，结果发现先作用逆时针是对的。

换句话说，明明应该是错的过程，偏偏结果对了；感觉是对的过程，结果错了。

当时很崩溃，不知道问题出在哪儿，然后就卡在这里想了两天。

嗯，最后一点一点的尝试，不停地举例子，不断地排除，最后发现我犯了一个极其简单的错误。

想清楚这件事之后，我似乎误打误撞的明白了魔方的本质。

反正在数学中，请善待你的好奇心，并珍惜你所有感觉不对劲的地方，因为这里可能蕴藏着很多宝藏。

总之你能想象吗？为了解一道很简单的题目，最后居然能扯到魔方的原理上去，这就是我最近一个有意思的学习经历。