如何评价2025八省联考数学多选最后一题？

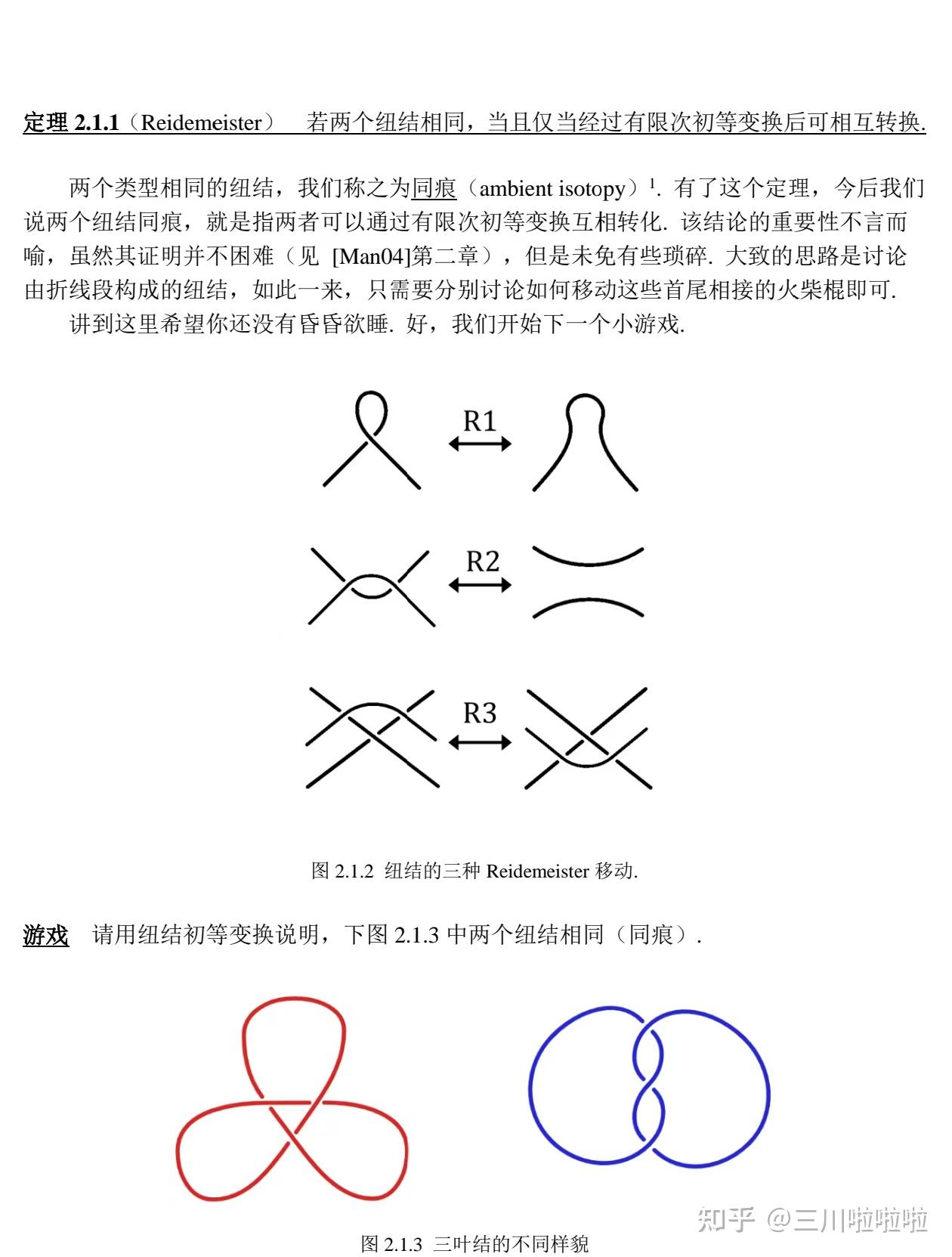
答案是ABD，有绳（鞋）子（带）摆一摆就能出来。最有迷惑性的实际上是BC，实际上只需要一、二步就能得出答案。动图展示如下——

---

B是无论如何得不到的，B是右手三叶结，C是左手三叶结，他们像一对孪生兄弟，彼此紧紧纠缠在一起。为区分两者，花费了无数数学家的时间与精力。

不过想严格区分平凡纽结（A）、以及左、右手三叶结（B与C）的区别，对中学生而言是不可能的。题干中就连两个纽结等价（同痕isotopy）的数学刻画都没有，所以只能通过空间想象以及直觉进行判断。

尤其是左右手三叶结，证明两者不同痕是很晚近的事了，所以做这个题最保险的策略是选AD，B弃选。

区分左右手三叶结有多难呢？就算你是一名普通的数学专业本科生，大概率也不会做。除非学校有专门的选修课，或者你通过某种渠道，私下了解纽结理解论。像纽结的众多不变量：纽结群、染色不变量、Alexander多项式、Alexander不变量、纽结能量、双曲体积……数学家开发出来的如此众多的工具都没办法解决这个看似简单的问题。Jones多项式算是相对简单的方法，但它是90年的菲尔兹……

对于不了解纽结的中学生读者，我只能说这个并不怪大家。就当是命运中无数个的玩笑之一，如果你从中找到了乐子，那他至少没有那么无聊。

---

纽结最基本的特征就是交叉点的数量，交叉数不超过3的只有平凡纽结，左、右手三叶结。

至于如何分辨左右手三叶结，需要了解交叉点的符号。直接说结论：

右手三叶结的三个交叉点符号是 ，而左手三叶结的三个交叉点符号是 。具体判断方法见下面图片。

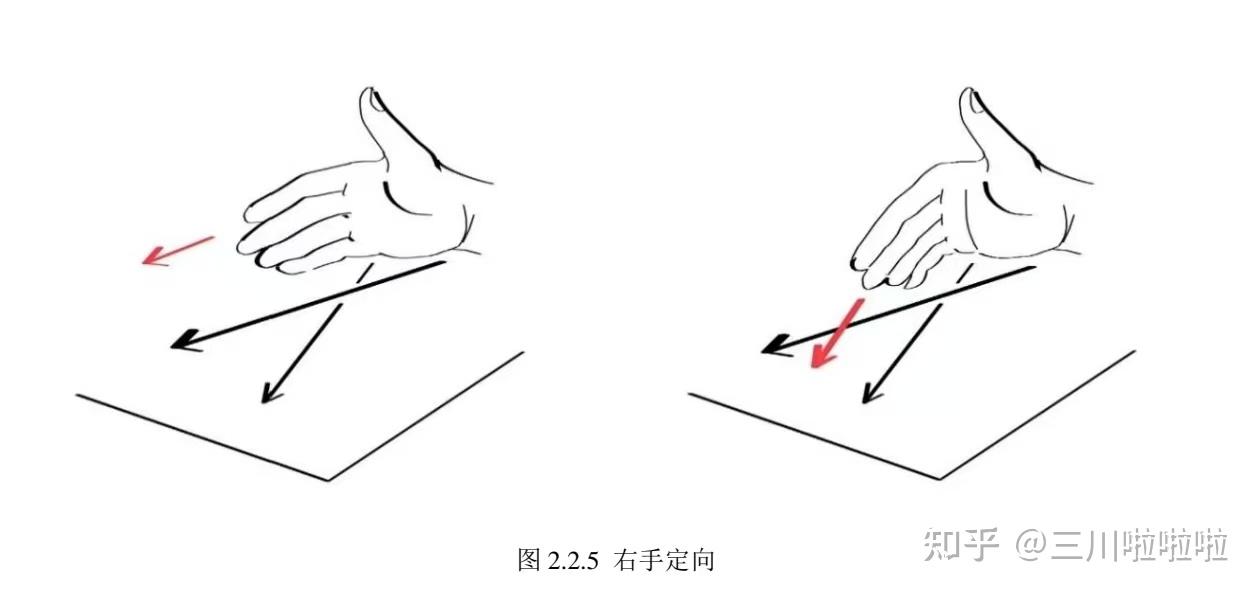
用Jones多项式可以严格区别左右手三叶结，详见

三川啦啦啦：纽结的故事4：Jones多项式

我写过一个程序，计算Kauffman多项式（和Jones就差一个因子）

三川啦啦啦：R语言：纽结的Bracket多项式

关于纽结的科普书书稿已经提交了，也不知道啥时候能出版。不过看姜伯驹院士的《绳圈中的数学》就够了，对于中学生而言。有关纽结理论的科普文章，我也写过很多——

为什么宇宙恰好是三维的，不是二维也不是四维？拓扑学有什么好玩的例子吗？顶级数学家有多厉害？拧了半圈和一圈半再粘合分别得到的莫比乌斯带，不能在不破坏的情况下互相转化，当用何种量来描述这种差异?为什么裤子前后穿反了不能通过“把裤腰旋转180度”的方式调整（而裙子可以）？

甚至我还写过相关内容的小说……

长篇创作马拉松第二季：有哪些推理满分或脑洞十足的故事让人大呼过瘾？

非常高兴能看到，同学们有机会接触、了解纽结理论。

这是一个非常深奥非常有趣的领域，而不单单是一道为难大家的题目。